Quantum computing, while relatively nascent, is on the precipice of revolutionizing the way we understand and interact with the digital world. At its core are the twin principles of superposition and entanglement, two concepts that challenge our everyday intuition and open the door to computing potentials beyond our current capabilities. But what are these principles, and why are they crucial in the quantum realm? This section will lay the foundation for our exploration into these groundbreaking concepts.
Classical vs. Quantum
To truly grasp the innovations of quantum mechanics, we must first understand the world of classical physics and computing. In the classical realm, the smallest piece of data is a bit, which can be in one of two states: 0 or 1. Computers, from the earliest to the most advanced, perform operations using combinations of these bits, forming the digital backbone of the world as we know it.
Quantum computing, on the other hand, introduces a new player to the game: the qubit. Unlike classical bits, qubits can exist in a state that is a combination of 0 and 1 simultaneously, thanks to superposition. Furthermore, qubits can be deeply interconnected, such that the state of one qubit can instantly affect another, no matter the distance between them. This phenomenon is known as entanglement.
| Feature | Classical Bits | Qubits |
|---|---|---|
| States | 0 or 1 | Superposition of 0 and 1 |
| Connectivity | Independent | Can be entangled with other qubits |
| Operations | Logical gates (AND, OR, NOT) | Quantum gates |
The World of Bits vs. Qubits

As we venture further into the quantum realm, it’s crucial to draw a distinction between the fundamental building blocks of classical and quantum computing: bits and qubits.
Understanding Classical Bits
In the digital universe, the bit is the atomic unit of data. Imagine a light switch; it’s either in the “off” (0) or “on” (1) position. Every piece of digital information, be it a photo, an email, or a webpage, is ultimately broken down into these binary states when processed or stored by a computer.
Classical computers operate using logical gates. These gates take in bits as inputs and produce outputs based on logic operations such as AND, OR, and NOT. For instance, an AND gate would produce an output of 1 only if both its input bits are 1; otherwise, it would output 0.
Introducing the Qubit
Qubits, or quantum bits, are the heart and soul of quantum computing. While they can represent a 0 or a 1 like classical bits, their true power lies in their ability to be in a superposition of both these states simultaneously. To visualize this, think of a spinning coin. While in motion, it’s neither heads nor tails but a blur of both. That “blur” captures the essence of superposition.
Moreover, qubits can be entangled, a phenomenon where the states of two qubits are interdependent. If you measure one qubit of an entangled pair, you instantly know the state of the other, irrespective of the distance between them. This mysterious linkage is one of the most perplexing and intriguing aspects of quantum mechanics.
| Feature | Classical Bits | Qubits |
|---|---|---|
| States | 0 or 1 | Superposition of 0 and 1 |
| Dependency | Independent | Can become entangled with other qubits |
| Operations | Logical gates | Quantum gates operating on probabilities |
Superposition: Beyond 0s and 1s

As we’ve touched upon, the principle of superposition allows quantum bits, or qubits, to exist in multiple states simultaneously. This concept stands in stark contrast to classical computing, where a bit must definitively be in a state of either 0 or 1. But what is superposition truly, and how does it work? Let’s dive deeper.
The Essence of Superposition
Picture a balanced seesaw in a playground. Instead of tilting completely to one side or the other (representing a 0 or a 1), it hovers in mid-air, balanced in an indeterminate state. This imagery captures the essence of a qubit in superposition, holding both a 0 and 1 simultaneously.
Mathematically, a qubit’s state in superposition can be represented as:
∣ψ⟩=α∣0⟩+β∣1⟩
Here, ∣ψ⟩ denotes the state of the qubit, and α and β are complex numbers determining the probability of the qubit collapsing to either the 0 or 1 state upon measurement. The probabilities can be computed as ∣α∣2 for 0 and ∣β∣2 for 1.
Harnessing the Power of Ambiguity
The idea of a qubit being in multiple states at once may seem counterintuitive, but this very ambiguity holds the key to quantum computing’s prowess. Superposition enables quantum computers to process vast amounts of data simultaneously, allowing them to solve specific complex problems at speeds unimaginable for classical computers.
For instance, a quantum algorithm leveraging superposition could search an unsorted database of N items in approximately √N steps, a significant improvement over classical algorithms.
Collapse Upon Measurement
While superposition offers vast computational advantages, there’s a twist. When a qubit in superposition is measured, it collapses to one of its basis states (0 or 1). This means that, post-measurement, the superposed state’s full information cannot be directly accessed. Quantum algorithms must be cleverly designed to extract useful information despite this collapse.
Challenges with Superposition
Maintaining a qubit in a superposition state is no small feat. Qubits are extremely sensitive to their surroundings, and external factors such as temperature fluctuations or electromagnetic radiation can cause them to fall out of superposition, a phenomenon known as decoherence. Quantum error correction techniques and advances in quantum hardware aim to combat these challenges.
Entanglement: The Mysterious Quantum Connection
One of the most enigmatic and intriguing phenomena in the quantum world is entanglement. At its core, entanglement represents a profound connection between qubits, a bond that transcends distance and challenges our understanding of reality itself.
Introduction to Quantum Entanglement
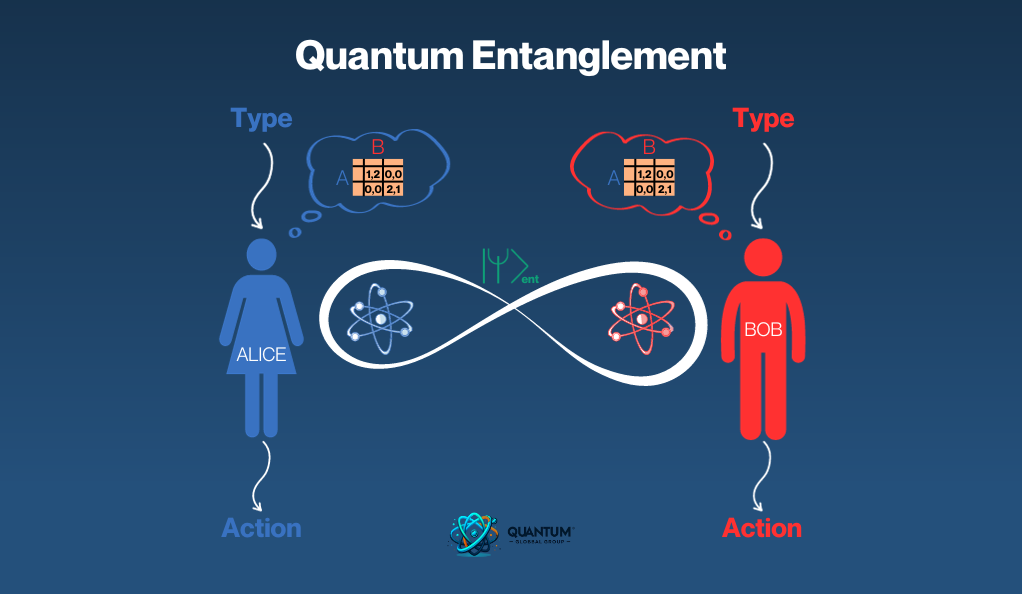
Imagine two particles, Alice and Bob. Once they become entangled, the state of Alice is directly related to the state of Bob, regardless of the space between them. This means if Alice is measured and found in a specific state, Bob’s state becomes instantly known, no matter how far apart they are. This phenomenon was so perplexing that even Einstein famously referred to it as “spooky action at a distance.”
The EPR Paradox and Bell’s Theorem: A Deeper Dive
The entanglement phenomenon led to a famous thought experiment in the 1930s known as the Einstein-Podolsky-Rosen (EPR) paradox. Einstein and his colleagues proposed this to challenge the completeness of quantum mechanics, arguing that there must be “hidden variables” explaining the correlation between entangled particles.
However, in the 1960s, physicist John Bell formulated a theorem (Bell’s theorem) which showed that if quantum mechanics is correct, then entangled particles are genuinely non-locally connected. Experiments conducted since then have consistently confirmed the predictions of quantum mechanics, sidelining the “hidden variables” theory.
Applications Leveraging Entanglement
Entanglement isn’t just a theoretical curiosity; it has practical applications:
- Quantum Cryptography: Leveraging entanglement, quantum key distribution can be achieved, where an eavesdropper’s presence can be detected due to the fundamental properties of quantum mechanics. This ensures ultra-secure communication channels.
- Quantum Teleportation: Not to be mistaken for science fiction-style teleportation, quantum teleportation involves the transfer of quantum information between particles over a distance. This is achieved using entangled particle pairs.
- Quantum Computing Algorithms: Several quantum algorithms, like the famous Grover’s and Shor’s algorithms, use entanglement as a key resource for speeding up computations and solving problems deemed hard for classical computers.
Conclusion
In our exploration of quantum computing, we’ve journeyed through the enigmatic realms of superposition and entanglement, peeling back layers of complex phenomena that promise to reshape our computational paradigm. While the road ahead is filled with challenges, the rewards, from groundbreaking algorithms to profound insights into the fabric of reality, are unparalleled.
Remember, quantum computing isn’t about rendering classical computing obsolete; it’s about augmenting our computational toolkit, offering solutions where traditional methods fall short. As we stand on this precipice of technological evolution, it’s clear that the quantum age isn’t just coming – it’s already here, unfolding one qubit at a time.




