In the ever-evolving landscape of technology, Quantum Machine Learning (QML) emerges as a groundbreaking intersection between quantum physics and machine learning. As we delve into the intricacies of this subject, it’s essential to understand its foundational concepts and the transformative potential it holds for the future of computation and artificial intelligence.
What is Quantum Machine Learning?

Quantum Machine Learning is the amalgamation of quantum algorithms with machine learning programs. At its core, QML seeks to harness the unique properties of quantum mechanics—such as superposition and entanglement—to process and analyze data in ways that classical computers cannot. This means that QML can potentially handle vast amounts of data at speeds previously deemed unattainable.
Significance of Quantum Machine Learning
The integration of quantum algorithms in machine learning is not just a mere fusion of two fields; it represents a paradigm shift in computational capabilities. Classical computers, bound by binary bits (0s and 1s), have limitations in processing the exponentially growing data in today’s digital age. Quantum computers, on the other hand, utilize qubits that can represent both 0 and 1 simultaneously, thanks to superposition. This allows for a vast computational space, making them inherently suitable for specific tasks in machine learning, cryptography, and optimization problems.
Moreover, the entanglement property in quantum mechanics enables qubits that are entangled to be correlated with one another—even when they are miles apart. This phenomenon can be harnessed in machine learning algorithms to improve data synchronization and processing.
Integration of Quantum Algorithms in Machine Learning
The most common use of QML refers to machine learning algorithms designed for the analysis of classical data but executed on a quantum computer. This approach, termed “quantum-enhanced machine learning,” leverages the power of qubits and quantum operations to improve computational speed and data storage capabilities. Such integration paves the way for hybrid methods that combine both classical and quantum processing, where computationally challenging subroutines are outsourced to quantum devices. These quantum routines can execute complex tasks faster and more efficiently than their classical counterparts.
Quantum-Enhanced Machine Learning
As we venture deeper into the realm of Quantum Machine Learning, one of the most compelling areas of exploration is quantum-enhanced machine learning. This approach seeks to capitalize on the inherent strengths of quantum mechanics to elevate the capabilities of traditional machine learning techniques.
Classical Data on Quantum Computers
While quantum computers are fundamentally different from their classical counterparts, they are not intended to replace them. Instead, they offer a complementary set of tools. One of the most promising applications of quantum computers is the analysis of classical data. By encoding classical data into quantum states, quantum algorithms can process and analyze this data in parallel, leveraging the power of superposition. This parallel processing capability can lead to significant speed-ups for specific algorithms, especially those that involve searching large databases or optimizing complex functions.
Hybrid Methods: Combining Classical and Quantum Processing
The true potential of Quantum Machine Learning may lie in hybrid methods that seamlessly integrate classical and quantum processing. In these systems, a classical computer handles tasks it’s optimized for, such as data preprocessing and certain computational tasks. In contrast, a quantum computer takes on the more computationally intensive subroutines, especially those that can benefit from quantum parallelism.
For instance, consider a machine learning model that requires the inversion of a large matrix—a task that grows exponentially more challenging as the matrix size increases. In a hybrid system, the classical computer could handle tasks like data input and output, while the quantum computer could efficiently invert the matrix.
| System | Strengths |
|---|---|
| Classical Computer | Data storage, preprocessing, user interface, and certain computational tasks. |
| Quantum Computer | Parallel processing, optimization problems, matrix inversions, and quantum simulations. |
Advantages of Quantum-Enhanced Techniques
- Speed: Quantum algorithms can offer exponential speed-ups for specific problems compared to classical algorithms.
- Parallelism: Thanks to superposition, quantum computers can process vast amounts of data simultaneously.
- Efficiency: Quantum systems can handle tasks that are currently infeasible for classical computers, such as simulating quantum systems or optimizing large functions.
Applications of Quantum Machine Learning
The fusion of quantum mechanics and machine learning has given rise to a plethora of applications that are set to redefine the boundaries of computational science. Let’s delve into some of the most promising applications of Quantum Machine Learning.
Quantum Associative Memories and Pattern Recognition
One of the earliest applications of quantum computing in machine learning was in the realm of associative memories. Quantum associative memory (QAM) algorithms can recognize patterns and retrieve associated data at speeds that outpace classical counterparts. By leveraging quantum parallelism, QAM can search through vast databases simultaneously, making it particularly useful for tasks like image and voice recognition.
Quantum Binary Classifier
Classification is a fundamental task in machine learning, where data is categorized into predefined classes. Quantum binary classifiers take this a step further by employing quantum algorithms to classify data points more efficiently. By encoding data into quantum states and using quantum interference, these classifiers can achieve higher accuracy rates and faster processing times, especially for large datasets.
Quantum-Enhanced Reinforcement Learning
Reinforcement learning involves an agent learning to make decisions by interacting with an environment. Quantum-enhanced reinforcement learning harnesses the power of quantum systems to process information about the environment more rapidly. This can lead to agents that learn optimal strategies faster and more effectively than those trained using classical methods.
Quantum Data Compression and Encryption
The principles of quantum mechanics can also be applied to data compression and encryption. Quantum data compression algorithms can represent vast amounts of information using fewer qubits than classical bits. On the encryption front, quantum key distribution ensures ultra-secure communication, leveraging the principles of superposition and entanglement to detect eavesdroppers.
Drug Discovery and Healthcare
One of the most exciting applications of Quantum Machine Learning lies in the field of healthcare. Quantum algorithms can simulate complex molecular structures, paving the way for drug discovery and personalized medicine. By analyzing genetic data and simulating molecular interactions at a quantum level, researchers can identify potential drug candidates and treatment pathways more efficiently.
| Application | Description |
|---|---|
| Quantum Associative Memories | Rapid pattern recognition and data retrieval. |
| Quantum Binary Classifier | Efficient data categorization using quantum interference. |
| Quantum Reinforcement Learning | Faster and more effective decision-making strategies. |
| Quantum Data Compression | Representing large datasets with fewer qubits. |
| Drug Discovery | Simulating molecular structures for efficient drug identification. |
Quantum Neural Networks
As we transition into the realm of neural networks, the fusion of quantum mechanics with this domain offers a tantalizing glimpse into the future of artificial intelligence. Quantum Neural Networks (QNNs) are a novel approach that seeks to harness the power of quantum mechanics to enhance the capabilities of traditional neural networks.
Understanding Quantum Neural Networks
At its core, a Quantum Neural Network is a quantum circuit that mimics the behavior of a classical neural network but operates on quantum data. Just as classical neural networks consist of layers of interconnected neurons, QNNs consist of layers of quantum gates that manipulate qubits. These qubits, thanks to the principles of superposition and entanglement, can represent and process vast amounts of information simultaneously.
Quantum Convolution Neural Network (QCNN)
A significant advancement in the field of QNNs is the Quantum Convolution Neural Network (QCNN). Drawing inspiration from classical convolutional neural networks (CNNs) used in image processing, QCNNs apply quantum gates in a convolutional manner to quantum data. This allows them to detect patterns and features in quantum data with high efficiency, making them particularly suitable for tasks like quantum image recognition and quantum data analysis.
Advantages of Quantum Neural Networks
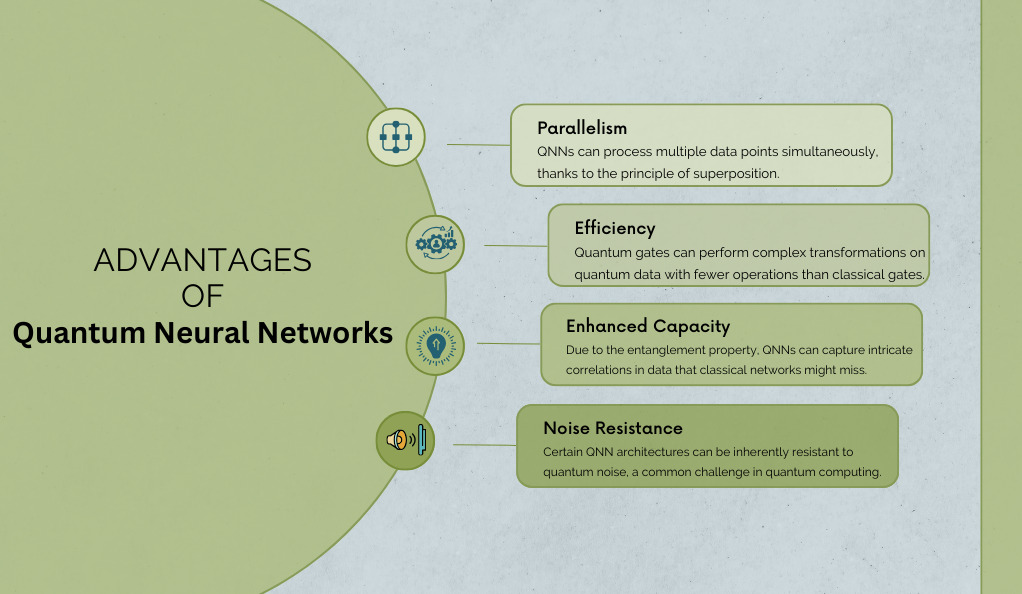
- Parallelism: QNNs can process multiple data points simultaneously, thanks to the principle of superposition.
- Efficiency: Quantum gates can perform complex transformations on quantum data with fewer operations than classical gates.
- Enhanced Capacity: Due to the entanglement property, QNNs can capture intricate correlations in data that classical networks might miss.
- Noise Resistance: Certain QNN architectures can be inherently resistant to quantum noise, a common challenge in quantum computing.
Challenges in Quantum Neural Networks
While QNNs hold immense promise, they are not without challenges:
- Training Difficulties: Training a QNN can be computationally intensive, especially as the network size grows.
- Quantum Hardware Limitations: Current quantum computers, especially NISQ (Noisy Intermediate-Scale Quantum) devices, have limitations in terms of qubit count and coherence time.
- Barren Plateaus: QNNs can encounter regions in their optimization landscape where the gradient is almost zero, making training extremely challenging.
Quantum Sampling Techniques
Sampling, a fundamental process in statistics and machine learning, involves selecting a subset from a larger set of data to estimate properties about the whole dataset. Quantum mechanics introduces novel sampling techniques that can revolutionize the way we approach complex problems in AI.
The Essence of Quantum Sampling
Quantum sampling leverages the principles of superposition and entanglement to generate samples from probability distributions. Unlike classical sampling, where each sample is generated sequentially, quantum sampling can produce multiple samples simultaneously. This parallelism is achieved by preparing a quantum system in a superposition of states, each representing a possible sample.
Quantum Annealing and Its Applications
One of the most prominent quantum sampling techniques is quantum annealing. It’s a metaheuristic optimization method used to find the global minimum of a given function. Quantum annealing exploits quantum tunneling, allowing the system to jump out of local minima and explore the solution space more effectively.
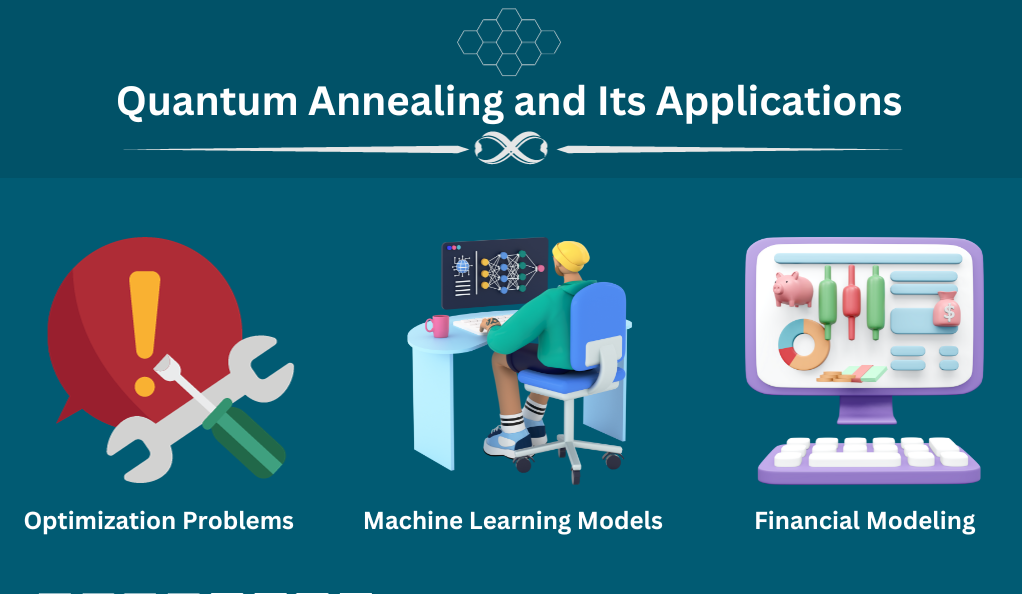
Applications of quantum annealing include:
- Optimization Problems: Tasks like the traveling salesman problem, where the goal is to find the shortest possible route that visits several cities and returns to the origin city.
- Machine Learning Models: Training models, especially deep neural networks, by finding optimal weights that minimize the loss function.
- Financial Modeling: Portfolio optimization, where the aim is to select the best combination of assets to maximize returns and minimize risks.
Boltzmann Machines and Quantum States
Boltzmann machines, a type of stochastic recurrent neural network, have a natural connection to quantum systems. Quantum versions of Boltzmann machines use quantum bits (qubits) instead of classical bits, allowing them to explore the solution space more efficiently. This makes them particularly suitable for tasks like pattern recognition and generative modeling.
Conclusion
As we stand on the precipice of a new era in computational science, the fusion of quantum mechanics and machine learning offers a tantalizing glimpse into the future. From the foundational principles of Quantum Machine Learning to the intricate workings of Quantum Neural Networks and the transformative potential of quantum sampling techniques, we’ve embarked on a journey through a landscape where the boundaries of what’s computationally possible are being redefined.
The applications of Quantum Machine Learning are vast, spanning from fundamental computational tasks to groundbreaking advancements in healthcare, finance, and beyond. While the challenges are real, stemming from both the nascent stage of quantum hardware and the inherent complexities of quantum algorithms, the potential rewards are immense.



